The Penultimate Post - A Paper Puzzle

My SLOG entry this will be my problem-solving entry. I am going to be writing about the paper folding problem we talked about back in week 3. I will try my best to follow George Pólya's steps to problem solving.

The problem statement:

Grasp one end of a strip of paper between the thumb and index finger of your right hand, and grasp the other end between the thumb and index finger of your left hand. Fold the strip of paper once, so that the end of the strip that was in your left hand now is on top of the end that was in your right hand, and the thumb and finger of your left hand now grips the fold at what was the middle. If you were to unfold the strip of paper now, it would have a single crease in a direction you might want to call "down."

If you carry out the fold several times, always folding the strip so that the end of the strip that is in the left hand is placed over the end that is in the right hand, what pattern of "up" and "down" folds do you get? For example, if I make two folds, I get a left-to-right pattern of "up," "down," "down."

Step 1: Understand the problem

The problem is to try and predict the sequence of ups and downs for a given number of times you fold a strip of paper in half. The paper should always be folded so that the end that was in your left hand is now on top of the end that was in your right hand because this will affect the results.

Step 2: Plan a solution

To solve this problem I folded the paper and wrote down the sequence for the first few folds. I then tried to see if there was a pattern in the sequence.

Step 3: Carry out your plan

Below are the sequences for the first 4 folds.

Folds	Sequence
1	D
2	UDD
3	UUDDUDD
4	UUDUUDDDUUDDUDD

Using 1 fold as our base case, the formula for this sequence would be to first take the previous sequence and mirror and flip it (the sequence backwards and D's become U's and vice-versa) and then append a 'D', and then append the previous sequence to the end.

The following is my implementation using recursion in Python.

def fold_sequence(folds):
    """ (int) -> str

    Return the sequence of the folds for a number of folds.

    Parameters:
    - folds: the number of times the paper is folded in half
    """

    if folds == 1:
        return 'D'
    else:
        prev_seq = fold_sequence(folds - 1)

        # reverse the previous sequence
        prev_seq_rev = prev_seq[::-1]
        prev_seq_rev = prev_seq_rev.replace("U", "d")
        prev_seq_rev = prev_seq_rev.replace("D", "U")

        # change the U's into D's and D's into U's
        prev_seq_rev = prev_seq_rev.replace("d", "D")
        return prev_seq_rev + 'D' + prev_seq


if __name__ == '__main__':

    while True:
        num_folds = input('Enter number of folds: ')

        # Convert into int
        num_int = int(num_folds)

        if num_int >= 1:
            print(fold_sequence(num_int))

You can test out the code at the following link: http://repl.it/1nu/4

Step 4: Review any solution you achieve

I think my solution is a correct one and the program I wrote should be able to convince someone that it gives the correct output.

To further extend this problem and further convince any more skeptics, I wrote a program in Python utilizing the ImageDraw module that takes an input for the number of folds and outputs the visual representation of the folds. The following are a few examples of the outputs from the program.

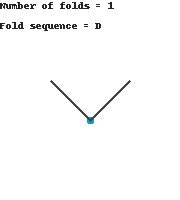1 fold

4 folds

6 folds

8 folds (Dropbox link)

10 folds (Dropbox link) Note: the original image is over 40,000 pixels long

To see the source code click here: https://pastee.org/k222h

Thank you for reading.

EDIT: I had a look around at a few other SLOGs to find some posts that others had made on this puzzle. I found a few posts here and here, and these posts all made the same solution I made so it is good to see that my solution seems to be the correct one.